地学のまも(@tigakunomamo)です
等級について説明していきますね。
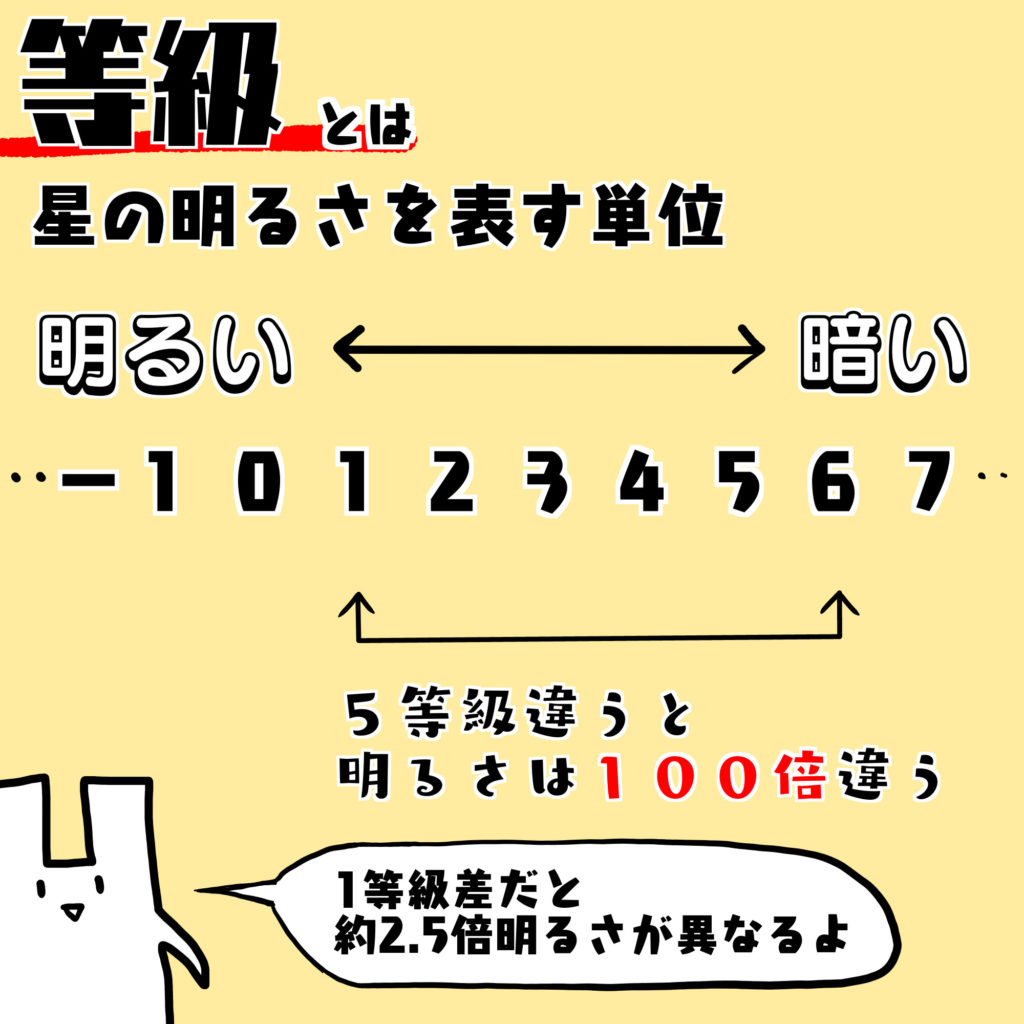
星の明るさを表す単位
数値が小さいほど明るい。
5等級差が100倍の明るさの違いになる。
数値が小さいほど明るい
明るいほど、等級の値は小さくなります。
逆に暗いほど、値は大きくなります。
明るいと等級がマイナス[-]になることもあります。
問:3等級の星と6等級の星では、どちらの方が明るいか?
答え:3等級の天体
5等級差が100倍の明るさの違い
5等級差がきっちり100倍の明るさの違いになることが、等級の定義です。
例えば、1等級の星と、6等級の星があれば、6等級の星に比べて1等級の星の方が、100倍明るいことになります。
1等級差であれば、約2.5倍の明るさの違いになります。
$${100}\approx{2.5}^5=2.5\times{2.5}\times{2.5}\times{2.5}\times{2.5}$$
問:2等級の星は7等級の星に比べて何倍明るいか?
答え:100倍明るい
解説:2等級と7等級では、ちょうど5等級差になるので明るさの違いが100倍になる。
問:2等級の星は12等級の星に比べて何倍明るいか?
答え:10000倍明るい
解説:2等級と12等級では、ちょうど10等級差になる。これは5等級差が2回あると考えられるので100×100で明るさの違いが10000倍になる。
ちなみに等級差と明るさの差の関係は次のようになります。
$$\frac{明るい星の明るさ}{暗い星の明るさ}=10^{\frac{2}{5}\times\left( {暗い星の等級-明るい星の等級} \right)}$$
見かけの等級と絶対等級
1つの星ごとに2種類の等級で表現できます。
それが見かけの等級と、絶対等級です。
地球から観測した明るさを等級にしたもの
星が10パーセク(32.6光年)の距離にあると仮定したときの等級
例えば地球から見える星で一番輝いているのは太陽で、見かけの等級は約-27等級です。
これは太陽が宇宙で一番明るく輝く星だからではなく、太陽が他の星に比べて一番近い距離にあるからです。
そのため、星本来の明るさを比べようと思ったら、すべての星を同じ距離に並べて、明るさを比べてやる必要があります。
星までの距離を10パーセクの位置にそろえて表した等級を絶対等級といい、絶対等級の大小で、星本来の明るさを比べることができます。
見かけの等級と星までの距離がわかれば絶対等級を計算できます。
$$M=m+5-5\log_{ 10 } d$$
$$M=m+5+5\log_{ 10 } p$$
M:絶対等級 m:見かけの等級 d:距離[パーセク] p:年周視差[秒]
等級の発祥
古代ギリシャの天文学者のヒッパルコスが考案しました。
有名な天体の等級
| 恒星名 | 見かけの等級 | 絶対等級 |
| 太陽 | -26.75 | 4.82 |
| シリウスA | -1.44 | 1.45 |
| ベガ | 0.03 | 0.6 |
| ベテルギウス | 0.42 | -5.5 |
| 北極星 | 2.0 | -3.6 |
| アークトゥルス | -0.06 | -0.3 |
太陽の見かけ等級では太陽は圧倒的に一番輝いていますが、絶対等級ではそこまで輝いていないことがわかります。














授業で使わせていただきました
匿名さん
コメントありがとうございます。
授業で使っていただけること、とても嬉しく思います。
こんなのがあったら良いなというものがありましたら、ぜひ教えてください。
太陽は東から西に動くのになぜ月は西から東に動くのですか?
教えてください。
中学生さん
コメントありがとうございます。
太陽も月も1日の動きで捉えると東から西に動きます。今回のご質問は日食の時などの月と太陽の相対的な動きということでしょうか?
実視等級0.46の星は何等星ですか?
kfさん
ご質問ありがとうございます。
見かけの等級を絶対等級に変換するには距離の情報が必要になりますので、その情報も教えていただけたら計算できます。
例題も付いていて分かりやすかったです。参考になりました。
纏寤夫 さん
コメントありがとうございます。
参考になったこと、とても嬉しく思います。
何等級ぐらいから肉眼で視認できなくなるのですか?
とある中学校の生徒 さん
コメントありがとうございます。
大変興味深い質問をいただきありがとうございます。
今の定義と異なりますが、大昔に等級の定義ができた頃には6等級までの星が肉眼で見える限界の星として定義されました。
ただ、肉眼で見える星は、その付近の明るさなどでも大きく変化します。そのため、実際には6等級の星を見ることはかなり難しいです。
国立科学博物館のHPにわかりやすい記事がありましたので、リンクを貼っておきます。よければご覧ください。
https://www.kahaku.go.jp/exhibitions/vm/resource/tenmon/space/seiza/seiza01.html#:~:text=1%E7%AD%89%E6%98%9F%E3%81%AE%E6%95%B0,%E3%81%A8%E3%81%84%E3%81%86%E3%81%93%E3%81%A8%E3%81%AB%E3%81%AA%E3%82%8A%E3%81%BE%E3%81%99%E3%80%82