マントルの上に地殻が浮いて、浮力と重力が釣り合っている状態こと

密度の小さい木片が密度の大きい水の上に浮かぶように、密度の小さい地殻が密度の大きいマントルの上に浮かんでいると考えることができます。
別の言葉で言い換えると、ある一定の深さにかかる圧力が一緒ということです。

アイソスタシーで取り上げられる問題は大きく2種類存在します。
1つ目は、氷河がとけた場所で、新たにアイソスタシーが成り立つためにどれくらい地面が隆起するかを計算する問題です。
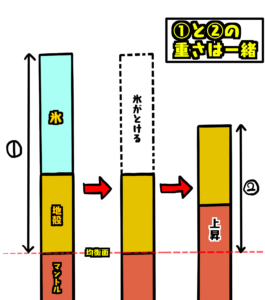
2つ目は、それぞれアイソスタシーが成り立っている2地点で厚みが不明な一方の地殻の長さを計算する問題です。
地殻の上に氷河がある状態でアイソスタシーが成り立っていたとする。その場所で氷河が全てとけた後、地面が隆起して再びアイソスタシーが成り立った。そのとき、地面はどれくらい隆起したか。有効数字2桁で答えよ。氷の密度は1.0\(g/{cm}^3\)、地殻の密度は2.8\(g/{cm}^3\)、マントルの密度は3.3\(g/{cm}^3\)とする。
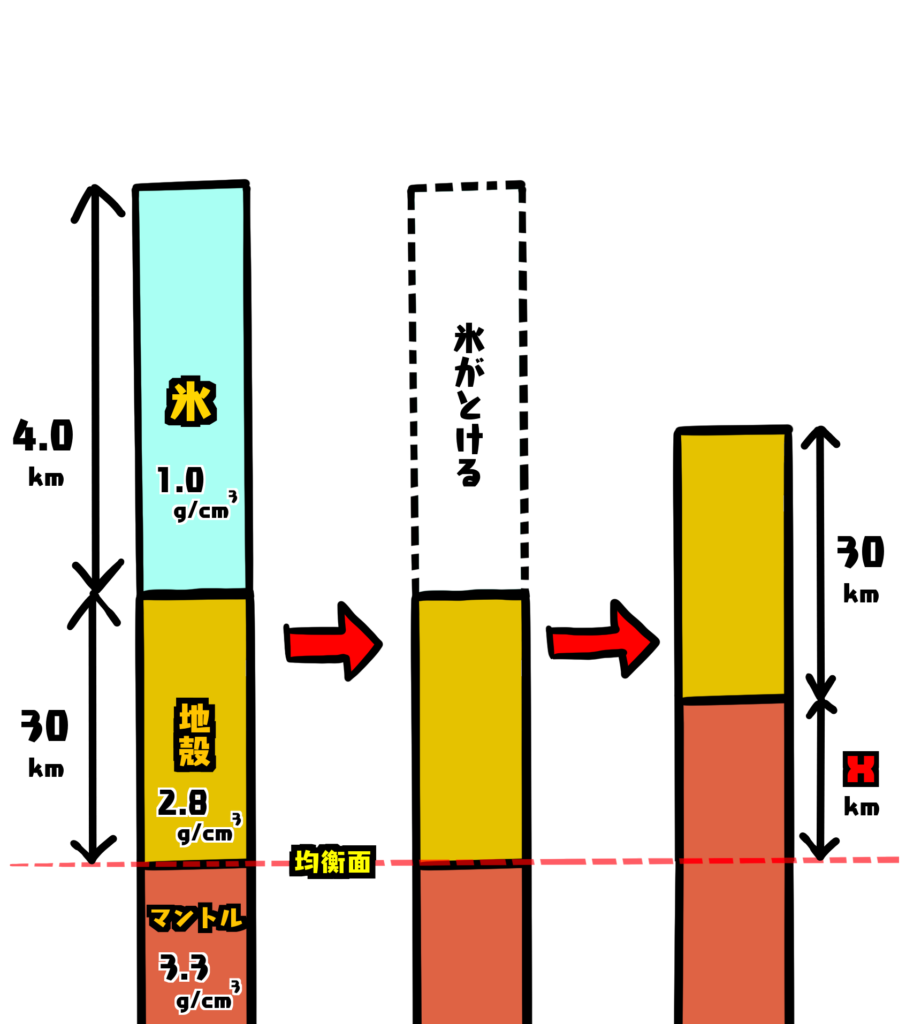
解き方
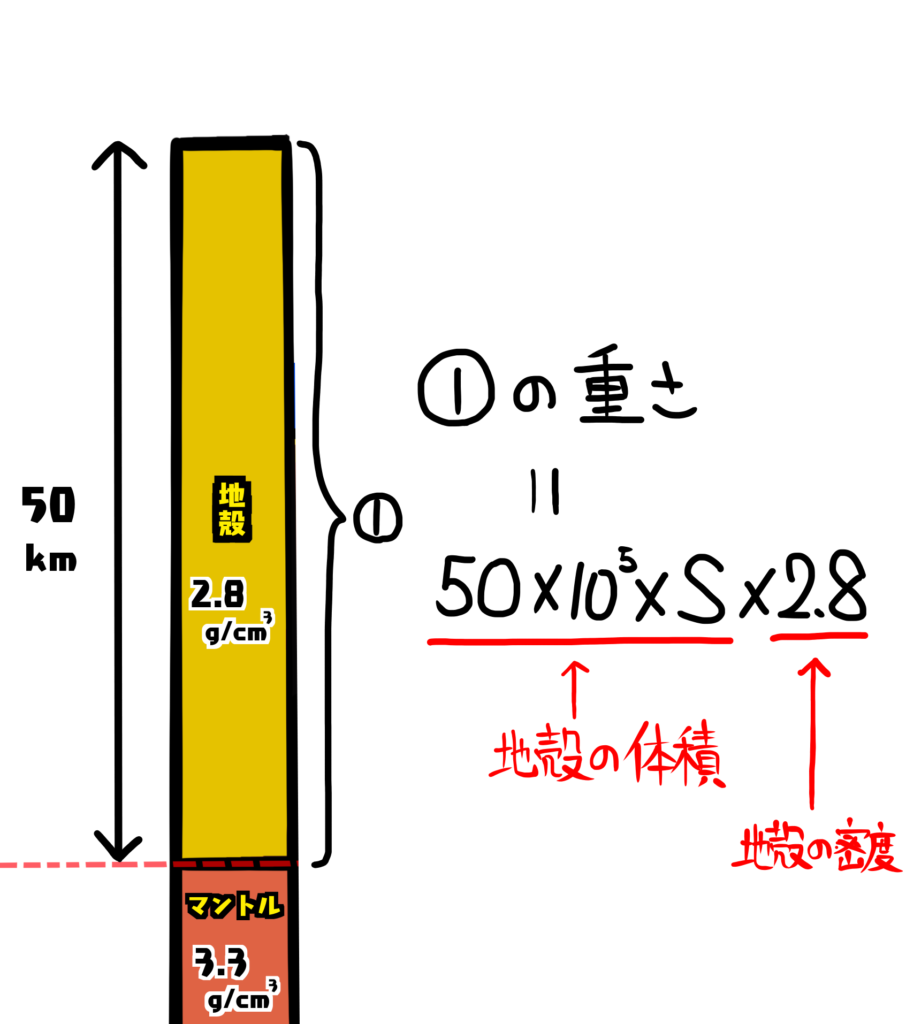
アイソスタシーが成り立っていると言うことは次の1と2の重さが一緒ということです。

①と②との重さはそれぞれ次のようになります。
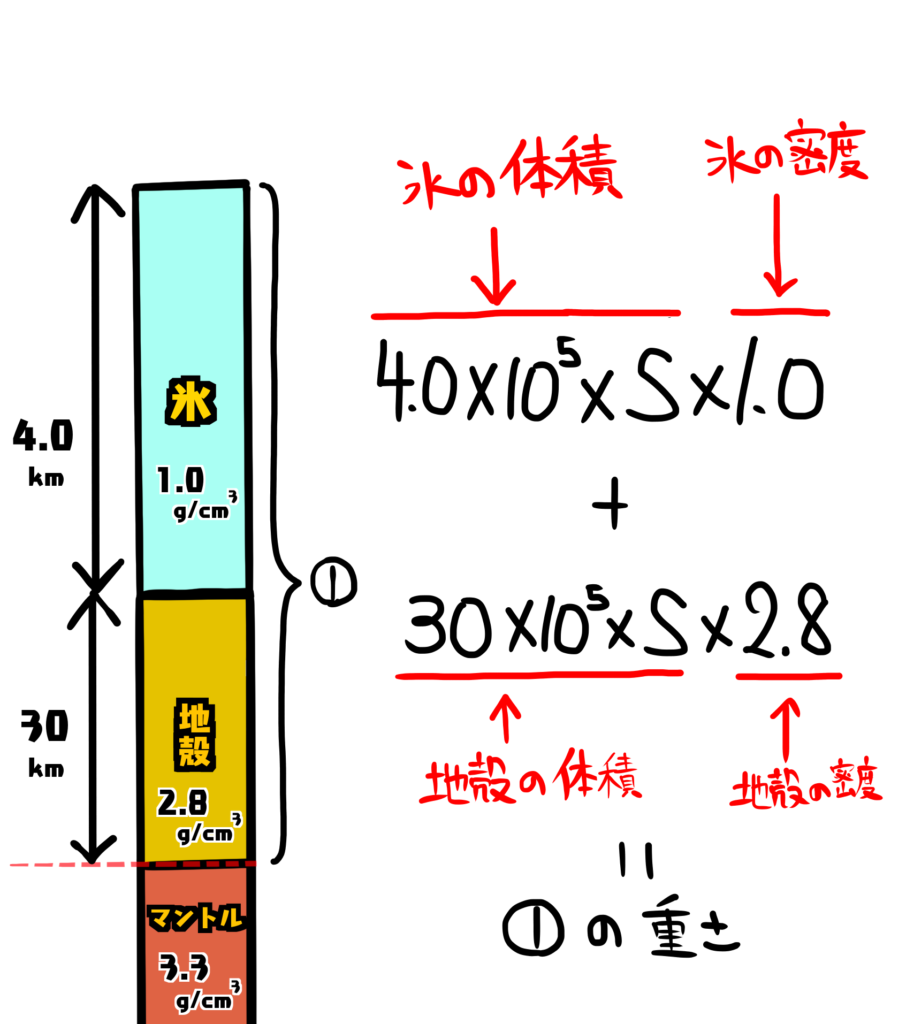
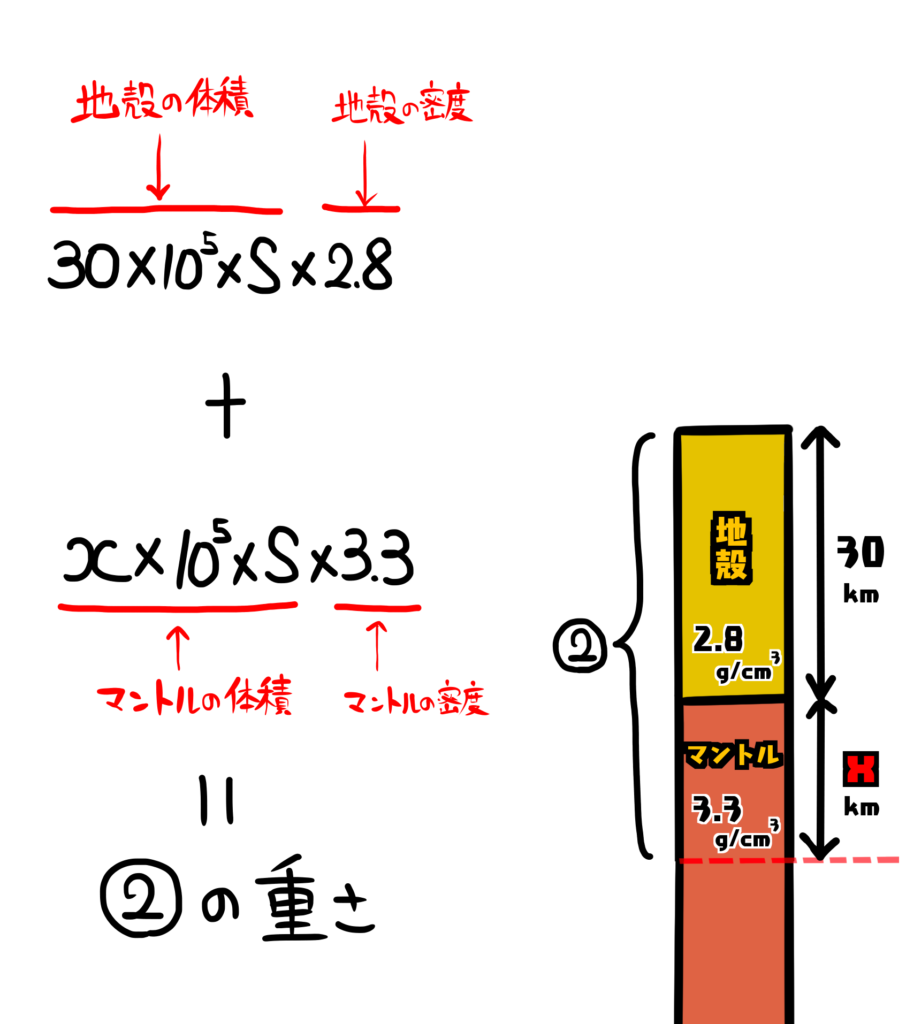
Sは面積[\({cm}^2\)]です。
①と②の重さが等しいので次のような式が成り立ちます。
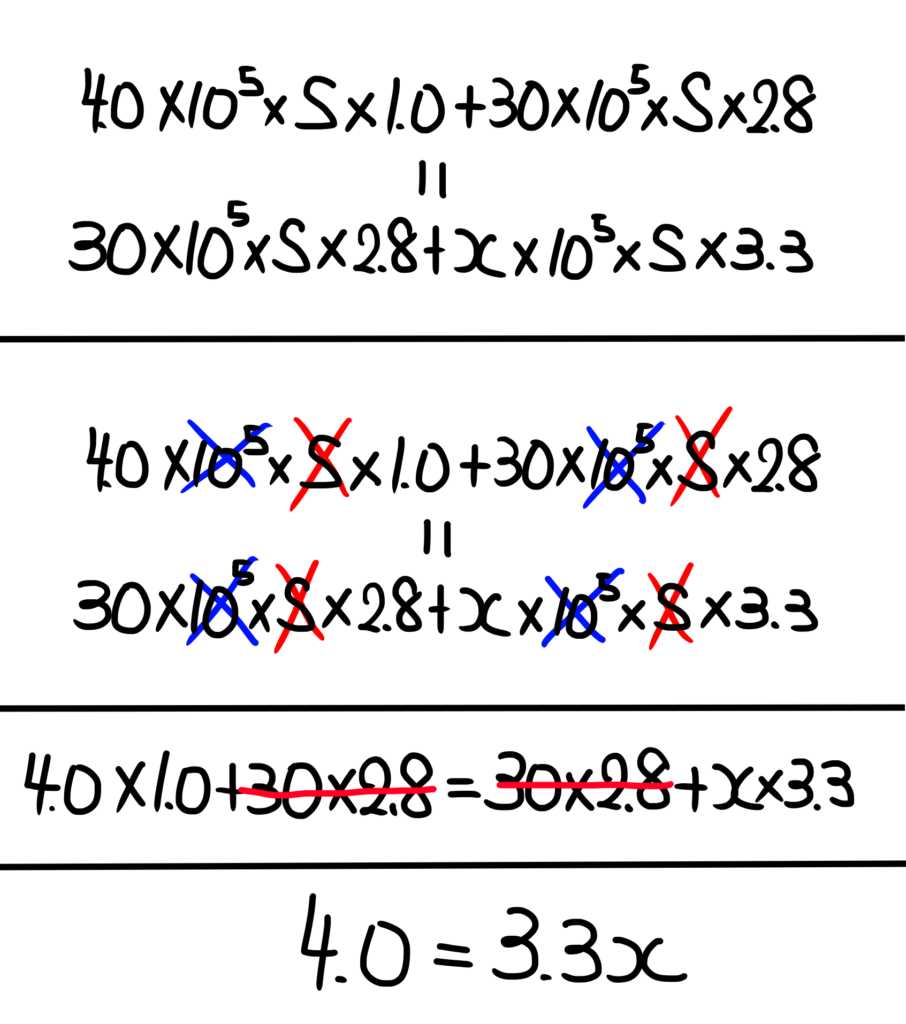
X=1.2121・・・
有効数字2桁なので、答えは1.2kmです。
答え
1.2km隆起する。
備考その1
だから実際の計算を解くときは10の5乗と面積Sは初めから省略して計算式を立てることが多いよ。
備考その2
ちなみにこのタイプの問題のときは地殻の厚さや重さは変化しないので、地殻のことは考えずに、氷の重さと同じだけのマントルが隆起すると考えると、よりシンプルに式を作れます。
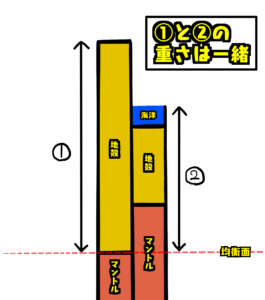
次の図の2地点はそれぞれアイソスタシーが成り立っている。図のxに当てはまる数値を有効数字2桁で答えよ。海の密度は1.0\(g/{cm}^3\)、地殻の密度は2.8\(g/{cm}^3\)、マントルの密度は3.3\(g/{cm}^3\)とする。
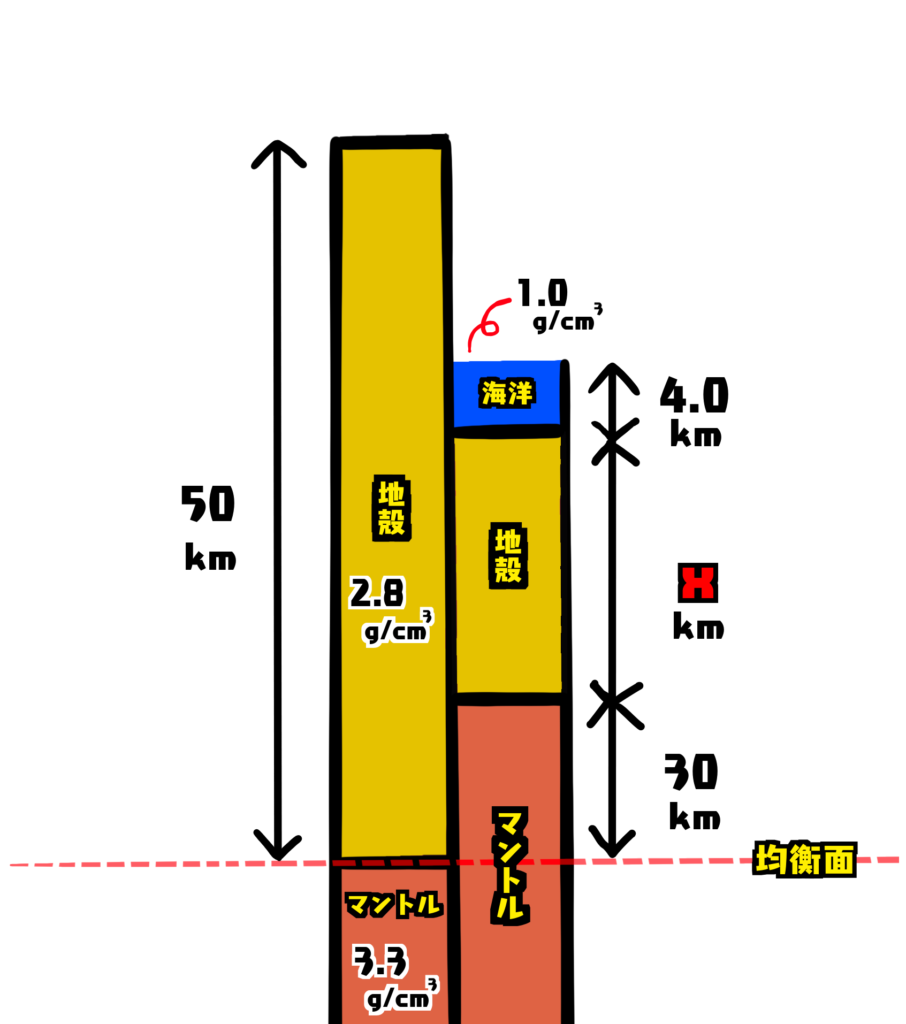
解き方
アイソスタシーが成り立っていると言うことは次の1と2の重さが一緒ということです。

①と②との重さはそれぞれ次のようになります。
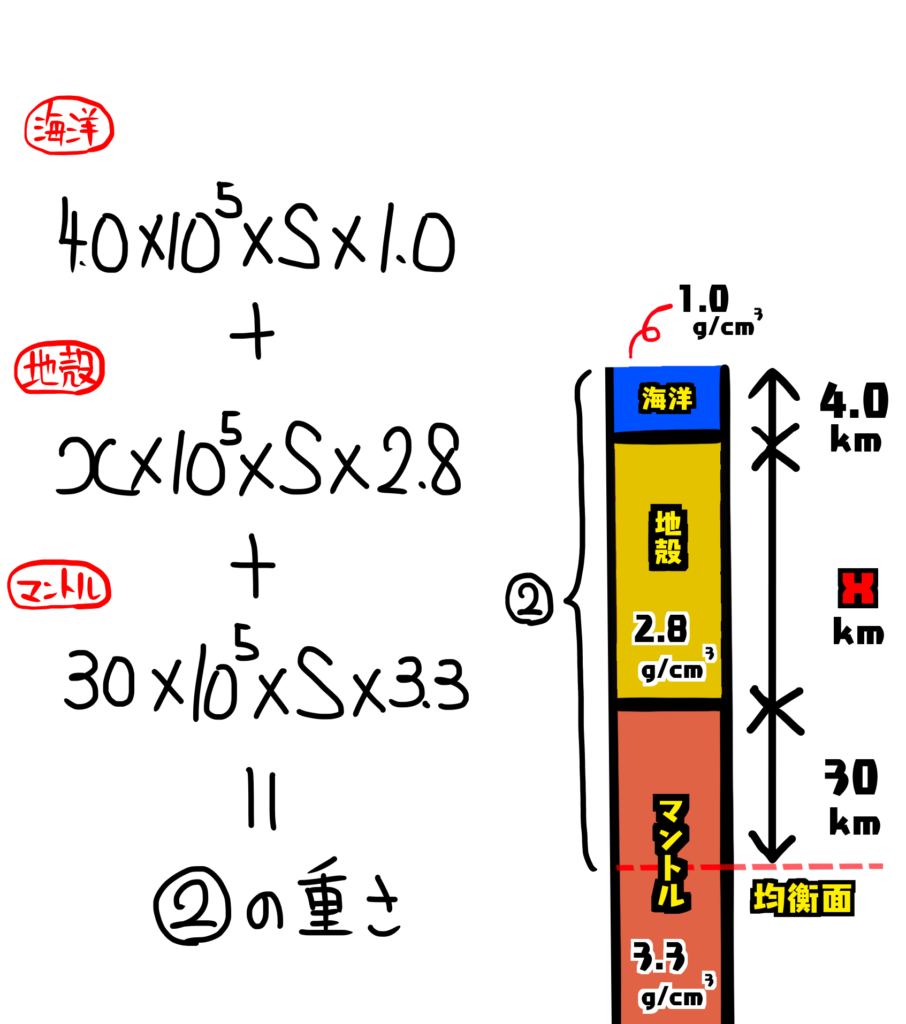
Sは面積[\({cm}^2\)]です。
①と②の重さが等しいので次のような式が成り立ちます。
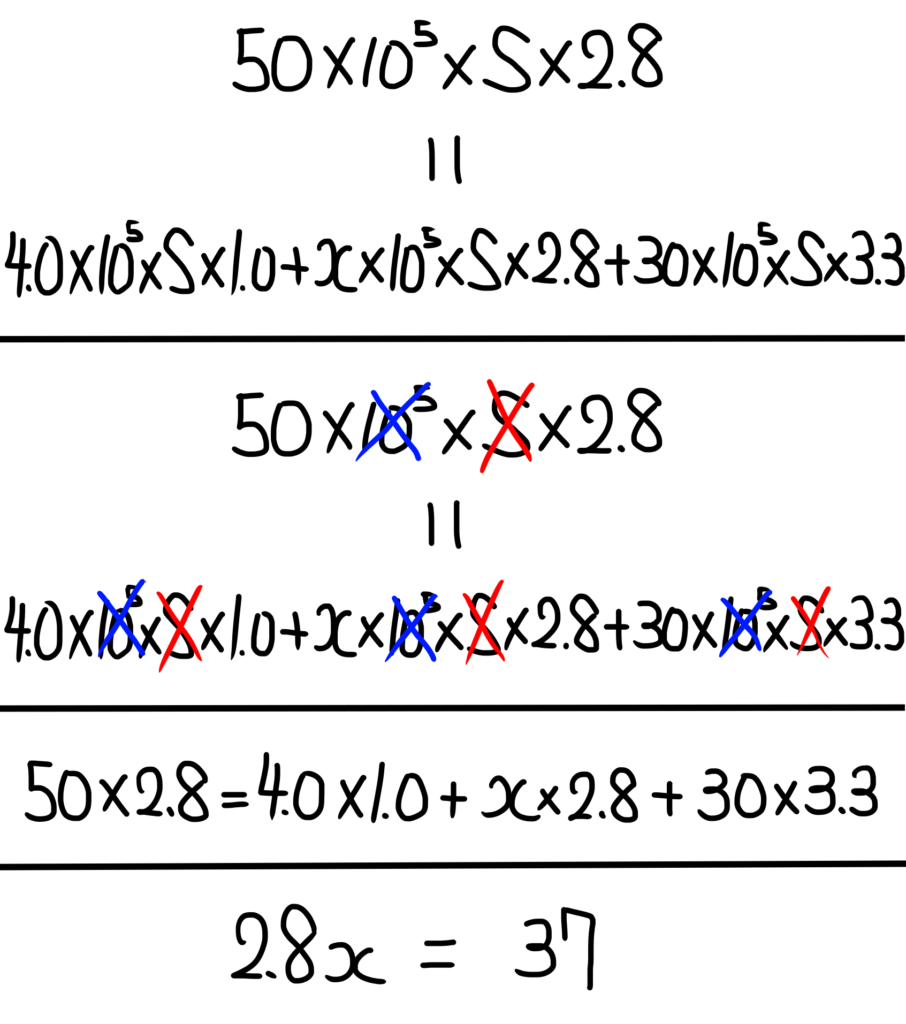
X=13.214・・・
有効数字2桁なので、答えは13kmです。
答え
xの長さは13km













アイソスタシーが成り立っているとフリーエア異常が0になる理由がいまだに理解できません(;_;)
コメントありがとうございます。
アイソスタシーが成り立っている状態は、ざっくりいうと、その場所の地下にある物質の重さがどの場所でも等しいという状態です。
その場合、場所ごとの重力の違いは高度によるものだけになります。そのため、アイソスタシーが成り立っていると、フリーエア補正だけで標準重力と一致して、フリーエア異常がなくなります。
わからない点があればまた再度ご質問くださいね。
高校生です
学校でアイソスタシー習ったけど意味わからなくて、でもこのサイトが分かりやす過ぎて理解出来ました!!!!!ありがとうございます
あ さん
コメントありがとうございます。
アイソスタシーの理解についてお役に立てたみたいで、こちらとしてもとても嬉しいです。
学校の授業でやっても分からなかったのですが、このサイトを見たら理解できました!
テストにも活かせそうです!!
だまーま さん
コメントありがとうございます。
記事が学習のお役に立てたこととても嬉しく思います。
学校で習いましたが、説明が難しく理解できずにいましたが、やっと意味を理解することができたので友達にも教えてあげようと思います。ありがとうございました。
gongorouさん
コメントありがとうございます。
お役に立てて、とても嬉しく思います。
もしアイソスタシーが成り立っていなかったらある一定の深さにかかる圧力が違うという認識であっていますか?もし違うのであればアイソスタシーが成り立っていない場合どのようになるのか教えていただきたいです。
ゆもさん
コメントありがとうございます。
おっしゃる通りアイソスタシーが成り立っていなかったらある一定の深さにかかる圧力が違うという認識であっています。
もし、氷床などが溶けた場合、地面の隆起や沈降には時間がかかるので、一時的にアイソスタシーが成り立たない状況が生まれることがあります。